El gesto, la mirada y el silencio rezuman preocupación. La voz encogida apenas puede susurrar el «buenos días» o «buenas tardes» protocolario y el acelerado «aquí le traigo los análisis, doctor…» que lo sigue, mientras el paciente se sienta en la silla y espera el veredicto. Algo grave, terrible e irremediable se esconde en esos papeles. La negrita y los asteriscos han hablado. El final debe estar cerca.
Pero el drama se transforma en escepticismo cuando digo:
—Bueno, pues está todo bastante bien….
—¿Cómo? ¡Pero si hay asteriscos en los análisis!
Imagino que la mayoría de personas deben pensar que les ha tocado al médico desequilibrado de turno, pero… es lo que hay…
Vamos a explicarlo con un poco de orden, con nuestra estadística rigurosa pero sencilla de la señorita Pepis y un poco de imaginación.
El problema
Lo habitual es que en una analítica ordinaria nos encontremos con asteriscos o valores en negrita. Y esto nos suele preocupar, pues pensamos que equivalen a tener alguna enfermedad o a padecer algo grave. El razonamiento es fácil: si alguno de estos valores está fuera de su sitio, es que algo va mal. Sin embargo, esta conclusión no es aplicable en todas las ocasiones y, de hecho, en un porcentaje notable de casos esos asteriscos y esas negritas no significan absolutamente nada.
¿De dónde salen los valores normales de las cosas?
Para explicar el origen de los valores normales, tenemos que entender qué es la campana de Gauss, una función matemática (que tiene forma de campana) y que usamos para decidir qué vamos a considerar normal y qué no.
Pongamos un ejemplo sencillo: yo me he medido el ancho de mi nariz y quiero saber si es «normal» o no. Puede que sea muy pequeño o muy grande (más probable en mi caso). ¿Cómo lo averiguo? ¿Qué entendemos por «normalidad»?
Pues lo que hacemos es medir la nariz a muchas personas (cuantas más mejor) y comparar todas esas medidas entre sí. Vamos a averiguar dos cosas: Lo primero es saber el tamaño promedio de la nariz y lo segundo cómo se agrupan las medidas alrededor de esa media. Luego veremos por qué esto es tan interesante. Vámonos pues a la plaza Mayor de Madrid y durante un año, a todos los transeúntes, les medimos la nariz con una regla…
Si se dejan, claro…
¿Todos somos iguales ante las matemáticas?
De entrada ya vemos que no es tan fácil hacer esa comparación de manera directa. Por un lado, hay niños, adultos y ancianos, y no tendría ningún sentido comparar mi nariz con la de un niño. También hay personas de raza negra y asiáticos, con diferencias morfológicas evidentes. Y hombres y mujeres…
Para que la comparación sea válida, debo seleccionar a una población lo más parecida a mí para que esas mediciones tengan sentido. En mi caso, el grupo sería de varones de 49 años y raza caucásica, por ejemplo. Cuanto más parecido tengan los individuos en todas sus variables, más razonable será compararme con ellos y no con otros. Por lo tanto, tras todas las mediciones, separo las de los varones caucásicos de 49 años.
Imaginemos que en ese grupo tengo al final 810 individuos con sus respectivas mediciones de narices que van desde 1 cm a 10 cm (claro que es un ejemplo, pero sirva la exageración absurda de estas medidas para entender el asunto).
Del número al dibujo
Con todas esas medidas hago una tabla, donde apunto cuántas personas hay para cada medición. Imaginemos para simplificar que todos tenemos medidas exactas entre 1 y 10 cm.

Lo que voy a obtener es algo parecido a esto: la mayoría de mediciones van a distribuirse alrededor de un valor central, que es la media aritmética de todas las mediciones. (En nuestro caso, 4,9, casi 5).
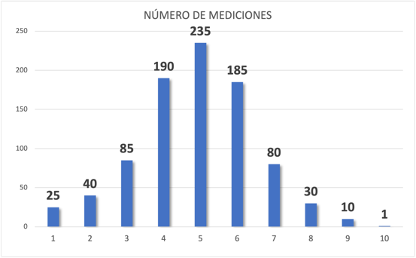
Aunque no todos tenemos la misma nariz, sabemos cuáles serían «normales» de manera instintiva: las que están dentro de unas medidas concretas donde entran la mayoría de las personas. Muy pocos tienen narices diminutas o gigantescas, ¿verdad? Vemos que sólo una persona tenía 10 cm de napia, por ejemplo. Aunque estos números sean absurdos, si nuestras mediciones fueran reales veremos que el tamaño normal estará entre unos valores alrededor de un tamaño medio central.
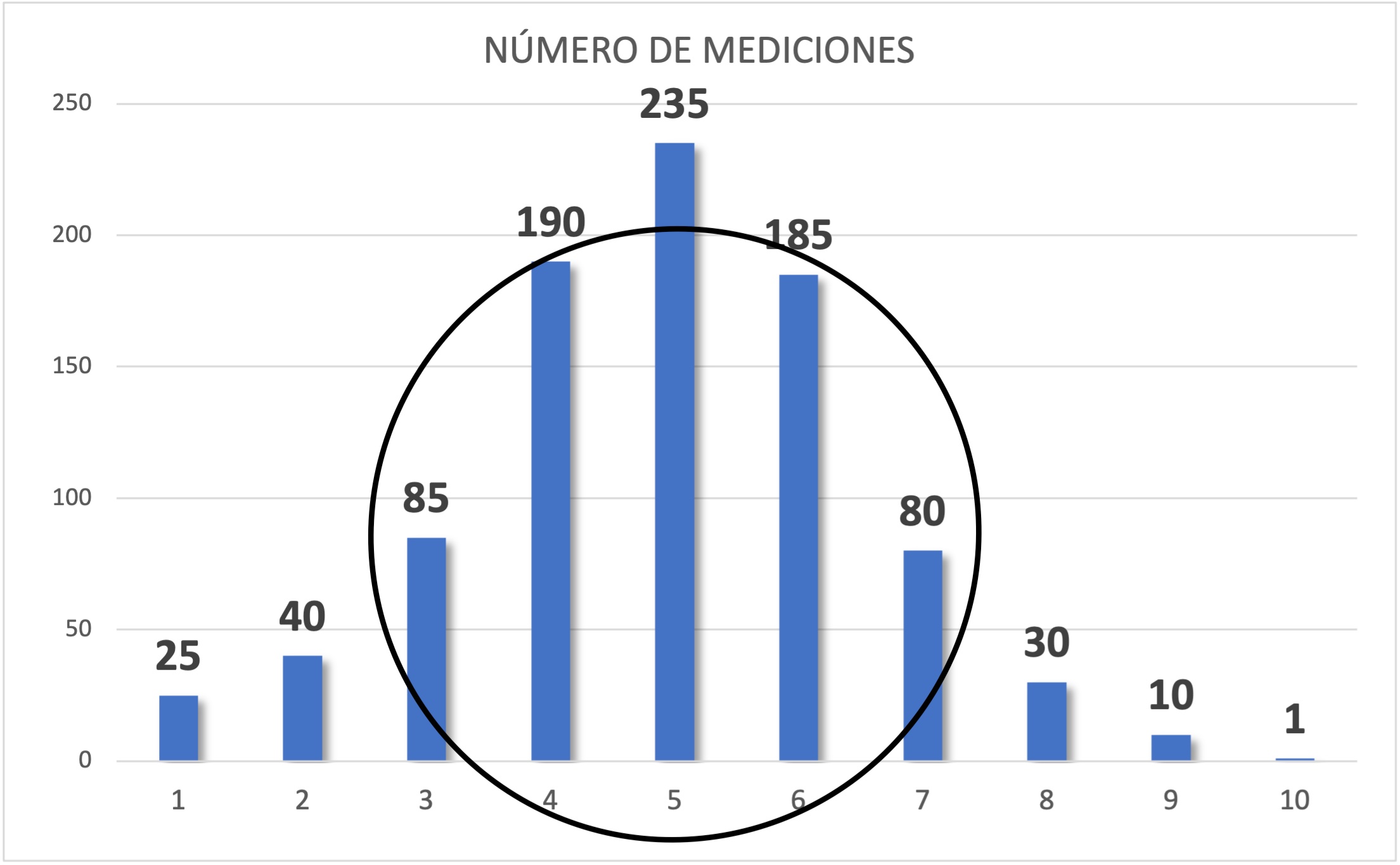
Nuestros números reflejan esa propiedad. Muy pocos tendrán narices extremadamente grandes o pequeñas, y a medida que nos acercamos a la media, el número de mediciones es mayor. Esto se conoce como distribución normal o campana de Gauss, y es una distribución matemática muy común para variables biológicas habituales, como la glucosa en sangre, la frecuencia cardiaca, etc. Es un modelo matemático que tiene propiedades muy interesantes que nos ayudan a establecer la normalidad
Números, porcentajes y probabilidades
Hemos pintado los valores absolutos, pero también podemos hacer una gráfica con los porcentajes de nuestras mediciones:
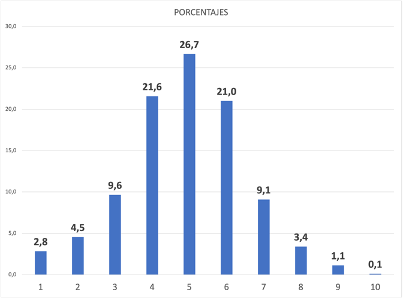
Si hacemos unas fórmulas matemáticas un poco más complejas, resulta que podemos dibujar una línea en forma de campana que representaría, para entendernos, los porcentajes de medición (las frecuencias medidas) si pudiéramos hacer un número de mediciones infinitas. Como siempre, alrededor de la nariz media es donde más porcentajes de narices hay, y a medida que nos alejamos, menos narices tendremos. El punto más alto de la curva es la mayor frecuencia obtenida.
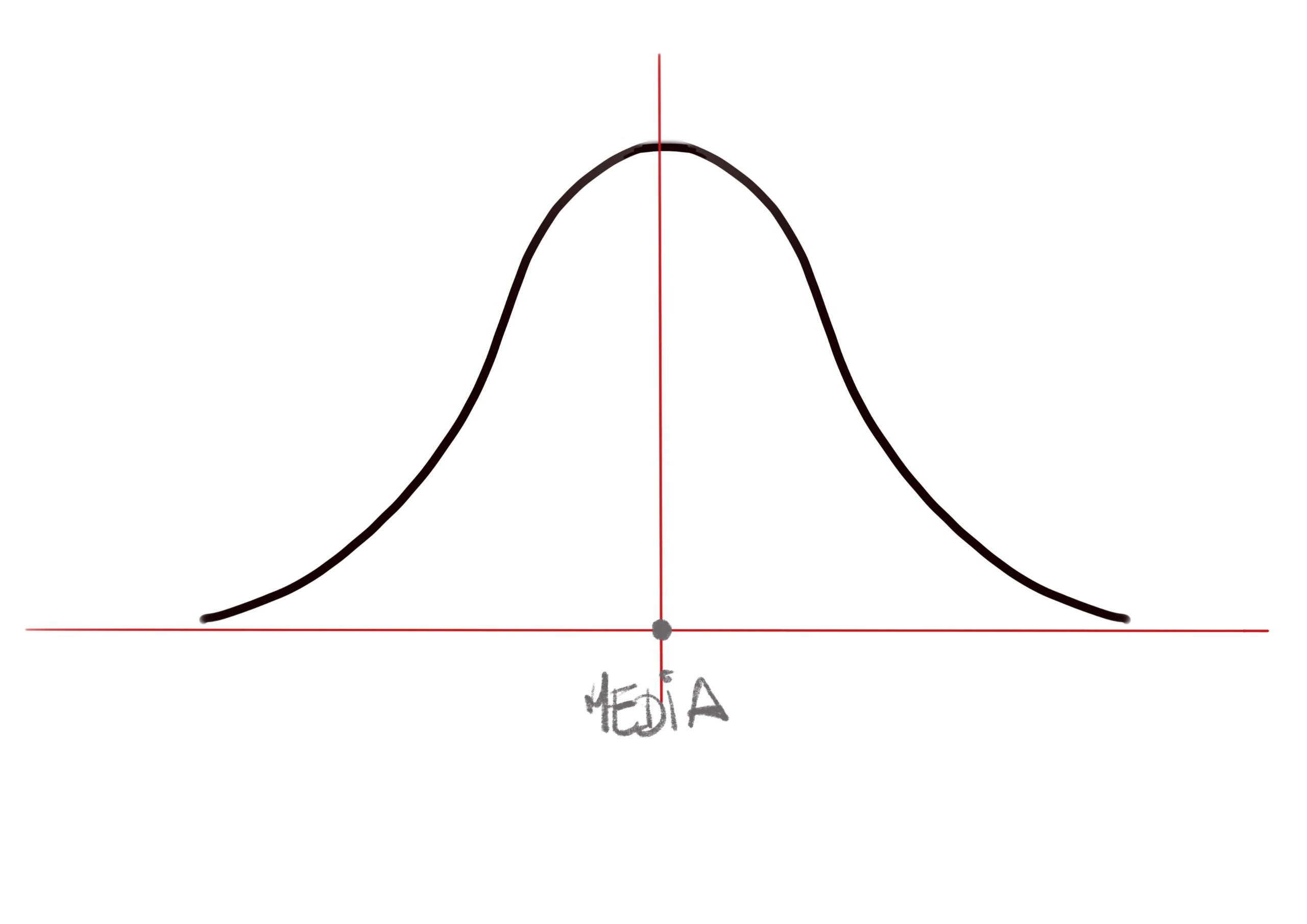
Si entendemos que el 100% de todas las personas están dentro de esa curva, y que el valor central es la media de las mediciones, podemos establecer conclusiones interesantes.
La curva de la campana es simétrica sobre el punto central que es el valor de la media. Esto significa que la mitad (el 50%) de las personas estarán a un lado u otro de esa media.
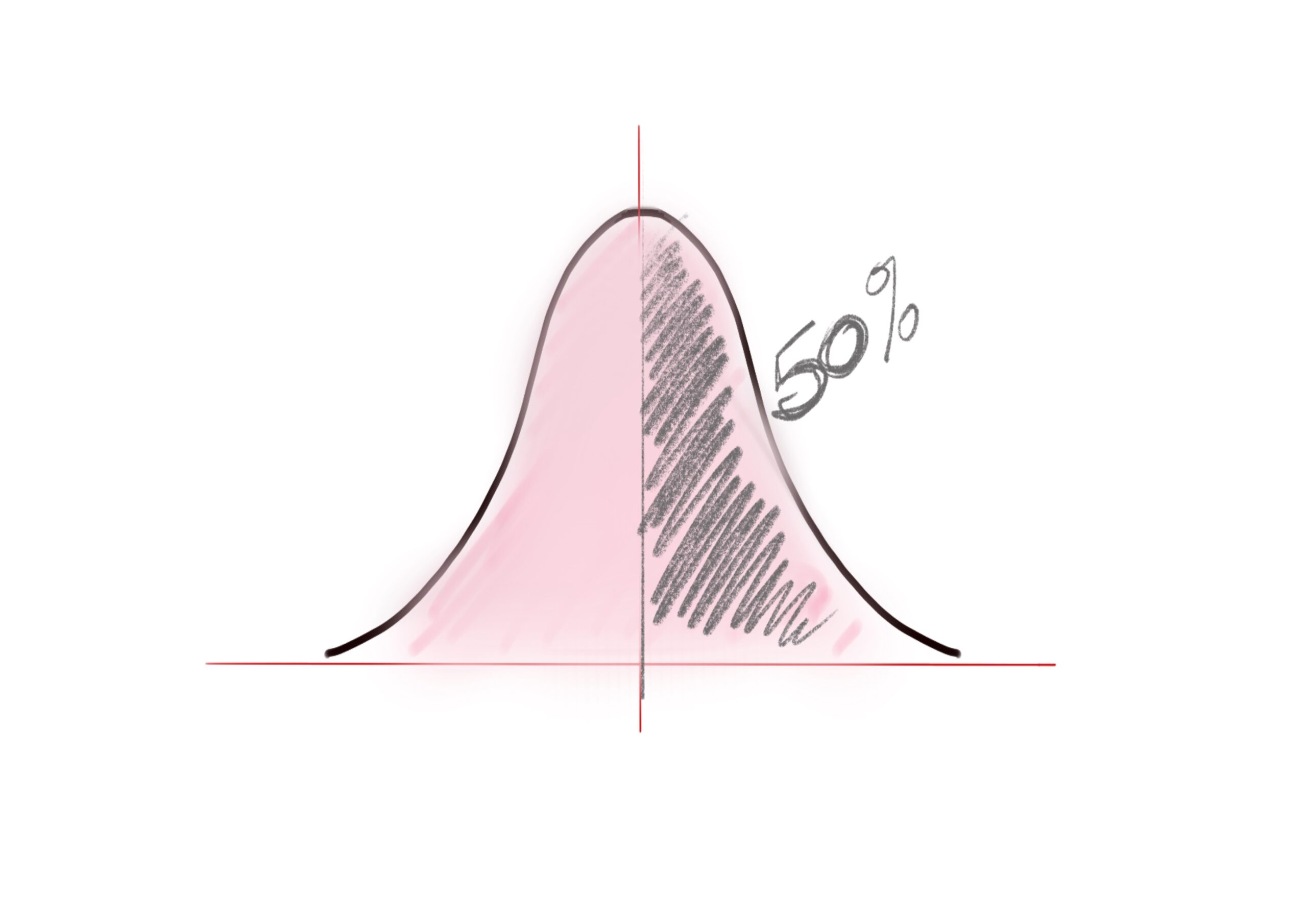
Estar por encima o por debajo de la media tampoco nos aclara si nuestra nariz es demasiado grande o muy pequeña. Para ello, tenemos que establecer unos límites a ambos lados de esa media. ¿Cuáles? Pues si nos fijamos un poco, vemos que la curva hace unas inflexiones en su trazado. La primera inflexión de esa campana corresponde a una desviación estándar, una medida muy interesante para entender por fin el tema de los asteriscos….
¿Qué es la desviación estándar y por qué tenemos que entenderla?
La desviación media es la media de todas las diferencias de los valores obtenidos en nuestras mediciones respecto a la media aritmética global. Como esta frase lo mismo no nos aclara nada, vamos a tratar de visualizarla para que se entienda.
Imaginemos que he medido sólo 10 narices.
4 miden 5 cm
2 miden 4 y otras 2 miden 6
una mide 7 y la última mide 3
La media es 5 porque (5+5+5+5+4+4+6+6+7+3)/10 son 5
4 narices se separan 0 cm de la media porque miden 5, y 5-5=0
4 narices se separan 1 cm de la media
2 narices se separan 2 cm de la media
¿Cómo calculo la media de todas esas desviaciones de la media de nuestra muestra?
Sumo todo y lo divido entre el número total de registros:
(0+0+0+0+1+1+1+1+2+2)/10 = 8/10 = 0,8
Si analizamos la media de todas las desviaciones de la media, tenemos la desviación media, 0,8 cm. Derivado de este concepto y con unas fórmulas un poco más complicadas surgen los cálculos de la desviación estándar, que en este caso es de 1,15 cm, un poco más que la desviación media, pero quedémonos con la idea de que este número nos indica la mayor o menor agrupación de datos alrededor de la media central.
Si la desviación estándar es muy grande, los valores estarán más dispersos respecto al valor central, si es pequeña, estarán más concentrados. Es decir, nos indica si la campana es más ancha o más estrecha. Dicho de otra manera: si es muy estrecha, la mayoría de valores no se alejarán mucho de la media, si es amplia, los valores estarán más alejados de ella.
Volvamos a la campana de porcentajes
Esos porcentajes se pueden entender también como probabilidades, pero para no enredar el asunto, quedémonos con la idea básica expuesta. Se cumple que si cogemos la media y le sumamos y restamos una desviación estándar, tenemos un grupo de población alrededor de esa media, cercano a ella, y esto nos interesa más que saber si estamos en el 50% superior o inferior, que en realidad tampoco dice nada.
Resulta que en la campana de Gauss, el 68,2% de todos los individuos estarán alrededor de la media y una desviación estándar por arriba y por debajo. Dicho de otra manera, si fuera válido nuestro ejemplo de 10 narices llevado a una población general, el 68,2% de los individuos de es población tendrán una nariz entre entre 5+/-1,15 cm., esto es, entre 3,85 y 6,15 cm.

Bueno, no está mal, pero si queremos estar un poco más seguro de la normalidad podemos aumentar esos porcentajes. Si añadimos dos desviaciones estándar respecto a la media, o sea, entre 2,7 y 7,3 cm, ahí tendremos al 95,4%.
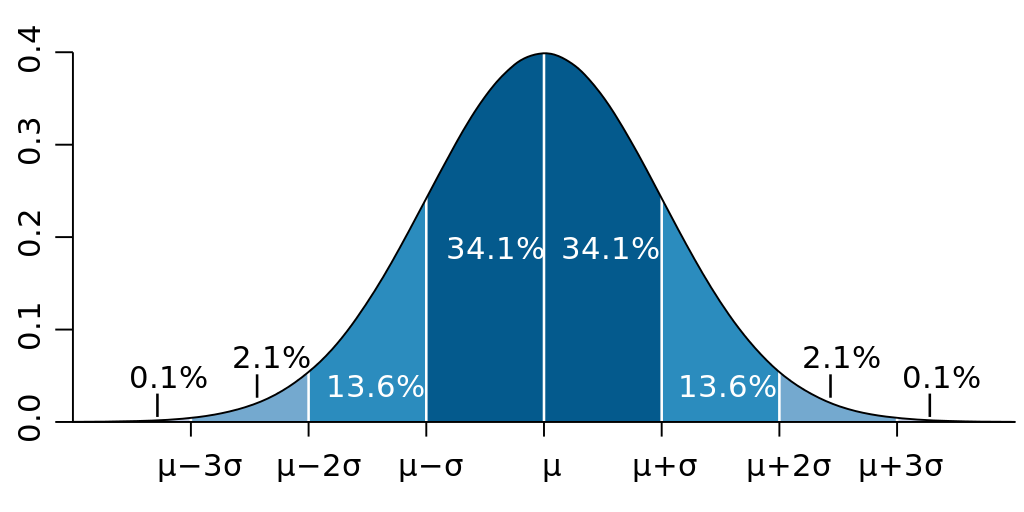
De Ainali – Trabajo propio, CC BY-SA 3.0
Dicho de una manera más sencilla: la gran mayoría de personas (95,4%) tienen una nariz que está entre 2,7 y 7,3 cm, y por eso asumimos que lo normal es tener una nariz entre 2,7 y 7,3 (dentro de nuestro sexo, raza, etc.). Es una decisión arbitraria pero que nos resulta muy útil de cara a determinar la probabilidad (que no la certeza) de que algo está bien o mal.
De esa manera establecemos los que consideramos valores normales de múltiples variables biológicas. Otro ejemplo: hemos tomado el pulso a millones de personas y, tras hacer la estadística, vemos que el 95,4% están entre 60 y 100 pulsaciones por minuto en reposo. De esa manera, establecemos 60 y 100 para establecer la “normalidad” del pulso en reposo. Da igual si alguien tiene 75 o 95, porque el 95,4% de las personas sanas están entre 60 y 100, así que esos valores son todos normales.
Por debajo de 60 o por encima de 100 resulta que sólo estaría el 0,6% de la población sana, relativamente muy poca gente, así que a partir de esos valores empezamos a preguntarnos si es que pasa algo. Ojo: el 0,6% de la población sana cae fuera de esos valores a los que consideramos normales, por lo que esos números, de entrada, no significan que algo vaya mal: sólo son personas sanas con valores fuera de la media entre dos desviaciones estándar de esa media, nada más.
Y llegan los asteriscos
En los laboratorios, para facilitar el trabajo de detección y que no se pase nada por alto entre tanto número, cuando un valor cae fuera de esos límites, se pone en negrita o con asterisco. Pero, ¿esto significa enfermedad o gravedad? ¡No necesariamente!
Un valor fuera de ese rango debe contextualizarse tanto en magnitud, como en la situación clínica del paciente. Muchos de esos datos de las analíticas que salen alterados no traducen “enfermedad” real, igual que una nariz más grande no necesariamente es una nariz enferma, o 105 de pulso no implica una taquicardia grave. Claro que es más probable que un valor muy alejado de la media y de su intervalo implique patología, pero siempre dentro de un contexto. Y otra cosa muy diferente y aún más importante es el significado clínico: aun siendo un valor fuera de lo normal, ¿hay que hacer algo con él?
Medicina de personas, no de números
La idea es que no tratamos analíticas sino personas. Esos valores indican parte del funcionamiento del sistema, pero no siempre traducen enfermedad ni esa enfermedad traduce necesidad de tratamiento. No es lo mismo una anemia (asteriscos en los hematíes) o una insuficiencia renal (asterisco en la creatinina y la urea) en una persona de 90 años con demencia senil que en una chica de veinte años. El significado y la trascendencia son muy diferentes aun siendo los números y los asteriscos idénticos.
Por ello, siempre hay que interpretar las pruebas en cada persona. Es más, en ocasiones, unas cifras normales no significa que no haya patología, igual que valores alterados pueden no significar nada, como los famosos «marcadores tumorales» o las elevaciones de transaminasas aisladas (que por cierto no sólo sirven para mirar cómo va el hígado). Incluso las máquinas precisan de calibraciones y nunca miden exactamente lo mismo. Cada valor tiene matices y significados que sólo los profesionales conocen y que el doctor Google pasa por alto. Tampoco es lo mismo tener un valor fuera de los límites que un conjunto de ellos, tendiendo que existir un patrón de coherencia entre esas desviaciones para que realmente esos análisis indiquen un problema concreto.
No conviene hacer medicina de asteriscos, sino medicina de personas. Las pruebas nunca son un fin en sí mismas, sino una fuente de información, nada más. Preguntemos y aclaremos con los profesionales qué significan las cosas y huyamos de interpretaciones peregrinas.
Si te ha gustado este post, sólo te pido que lo difundas y lo compartas en tus redes sociales favoritas sin miedo. Así llegará a más gente, que a su vez también lo compartirá en caso de que le guste. Google se dará cuenta, que lo vigila todo, y se lo enseñará a más y más gente…
De esta manera me haré multimillonario y podré invitarte a un café con pastas 😉
Mil gracias por compartir y comentar 🙂

